Analysing Households Below Average Income using R
This is an introduction to using the sample survey Households Below Average Income in the R Statistics Package. With this you have all you need to carry out analysis of the distribution of income in the UK using the world’s finest open-source software.
Available to download:
Introduction
Households Below Average Income is the premier UK survey source on household incomes. The name is slightly misleading: whilst the survey is used to produce official estimates of income poverty, it covers all UK households, not just those with low incomes. It can thus be used to study the whole income distribution, income inequality and inter-group differences in financial resources.
This note1 provides an introduction to analysing HBAI using the R
statistics package, showing how to reproduce some of the main published
analyses; there are references to the table and figure numbers of the
main report and supplemental tables2. This note assumes basic
knowledge of R, as well as of concepts used in income research such as
equivalisation and poverty thresholds3. It uses the survey package
for R, which will need to be installed before running the examples.
Survey design
The cases in HBAI are taken from the Family Resources Survey (FRS), which has been carried out annually since 1994/95 by the Department of Work and Pensions. The FRS currently has a sample of around 20,000 households in the UK. It has a complex multi-stage sampling design. This complicates the estimation of error in estimates, and this is covered briefly at the end of this note.
Getting access to HBAI
HBAI data4 are distributed by the UK Data Service
(http://ukdataservice.ac.uk). The data are free of charge, although
registration is required. The data files can be downloaded in various
formats; the TAB (tab-delimited format) can be read reliably with R’s
built-in read.delim function, or with faster alternatives such as
data.tables fread.
The standard data set has various measures applied to it to preserve the anonymity of respondents. This includes rounding-off money sums to the nearest pound, and suppressing fields that identify the location of respondents more closely than their region.
HBAI and the Family Resources Survey
Data for both HBAI and FRS are available. The HBAI data have a simpler format and include additional derived variables that are useful for calculating poverty measures, such as equivalisation scales. The FRS has a complex data file structure, but has much more detailed information on the characteristics of individual household members, sources of income and so forth. The cases in the two datasets are have shared serial numbers so that data can be matched from FRS to HBAI. It can thus be easier to start with HBAI, and then match in data from FRS as required.
Data file design
Each HBAI file represents one (financial) year. Each case in each file
represents a benefit unit, roughly equivalent to a “family””,
consisting of an adult, their spouse or partner, if any, and their
dependent children. A household consists of one or more benefit units
living together. In HBAI, a household is identified by the variable
SERNUM and each benefit unit within it is then numbered sequentially
by the variable BENUNIT.
Grossing Factors
The cases in HBAI each have a set of grossing factors or weights. Although each case is a benefit unit, by using the appropriate grossing factor totals for the number of adults, people, children, households and so on can be calculated. It is important to know what totals are required and to choose the appropriate grossing factor — see the User Guide.
Single-year analysis
Let’s get started with some single-year analysis of the contemporary
income distribution. First load the data file for 2012/13 and set up a
survey object with the weighting for all persons (GS_NEWPP). Most of
the published analyses use this grossing factor, presenting proportions
or counts of the whole UK population. The technical guide has a complete
list of available weighting variables.
### GETTING STARTED
library(survey)
# Change this to wherever your data are stored
hbai.data.dir <- "~/data/HBAI/HBAI1213/tab/"
# Load the source data
hbai <- read.delim(sprintf("%s%s",
hbai.data.dir,
"hbai1213_g4.tab"))
# Set up the survey design, using person weights
ppl.svy <- svydesign(id=~1,
data=hbai,
weight=~GS_NEWPP)
# Some alternative weights:
# GS_NEWCH - numbers of children
# GS_NEWPN - numbers of pensioners
Deciles of the whole income distribution (cf Table 2b, page 32)
Now to calculating some basic points (the mean, deciles) in the income
distribution of all people. Two key variables are S_OE_BHC and
S_OE_AHC which contain each benefit unit’s income, equivalised
according to the modified OECD scale, before and after housing costs,
respectively. Other equivalisation scales (e.g. McClements) are
available in HBAI; see the variable list provided with the
documentation.
### THE OVERALL DISTRIBUTION OF INCOME (cf Table 2b, p32)
# Mean before-housing-costs income - £535.52 / week
bhc.mean <- svymean(~S_OE_BHC, ppl.svy)
# Deciles of BHC income
bhc.deciles <- svyquantile(~S_OE_BHC, ppl.svy,
quantiles=seq(0.1, 0.9, 0.1) )
bhc.deciles
These values can be compared to the 2012/13 values presented on page 32 of the report, which give quintile group medians. The median of quintile 1 is the same as the first decile value calculated here, the median of quintile 2 the third decile, and so on.
| Decile | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| S_OE_BHC | 227 | 288 | 336 | 385 | 440 | 501 | 578 | 685 | 884 |
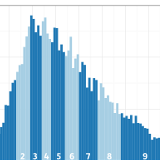
Charting the BHC income distribution (cf Chart 2.4/BHC, p28)
Now to reproduce a chart from the report, with the main published representation of the whole BHC income distribution. Whilst the chart design has shortcomings, such as chopping off a chunk of wealthy households on the right hand side, it gives a first impression of what the overall income distribution looks like. To reproduce this chart we first need to band the data:
### CHARTING THE INCOME DISTRIBUTION (cf Chart 2.4/BHC, p28)
# Group incomes up to £1,000 in £10 bands
hbai$bhc.inc.10grp <- cut(hbai$S_OE_BHC,
seq(0,1000,by=10),
right=FALSE, include.lowest=TRUE)
# Since we have added variables, survey design must be respecified
ppl.svy <- svydesign(id=~1, data=hbai, weight=~GS_NEWPP)
# Counts of all people in each band
bands.freq <- svytable(~bhc.inc.10grp, ppl.svy)
Then the ggplot2 package is used, which builds a complex chart like this from its constituent pieces. Those unfamiliar with and uninterested in using ggplot2 can, of course, skip this section.
# From here on, set up the data specifically for plotting,
# as per the chart in the HBAI report
# First make a data.frame for plotting
bands <- data.frame(ppl=bands.freq,
lower=seq(0,990,10),
upper=seq(10,1000,10) )
# Assign each band to one of of the deciles of the whole distribution
deciles.rnd <- signif(bhc.deciles,2)
bands$decile <- sapply(bands$upper, function(b) sum(b>deciles.rnd) + 1)
# Place the label for each decile in the middle of the relevant bands
dec.labels <- data.frame(dec=1:10,
x=(c(0,bhc.deciles) + c(bhc.deciles, 1000))/2)
# Actually create the plot, scaling to millions
library(ggplot2)
ggplot(bands)+
geom_rect(aes(xmin=lower, xmax=upper,
ymin=0, ymax=ppl.Freq/10^6,
fill=factor(decile%%2)) ) +
scale_fill_brewer("",type="qual", palette="Paired", guide=FALSE) +
scale_y_continuous("People (millions)",
limits=c(0,1.5),
expand=c(0,0)) +
scale_x_continuous("Equivalised BHC income (£/week, £10 bands)",
limits=c(0,1050),
breaks=seq(0,1000,100),
expand=c(0,0)) +
geom_text(data=dec.labels, aes(x=x, y=0.05, label=dec),
colour="white", fontface="bold", size=10/14*5)
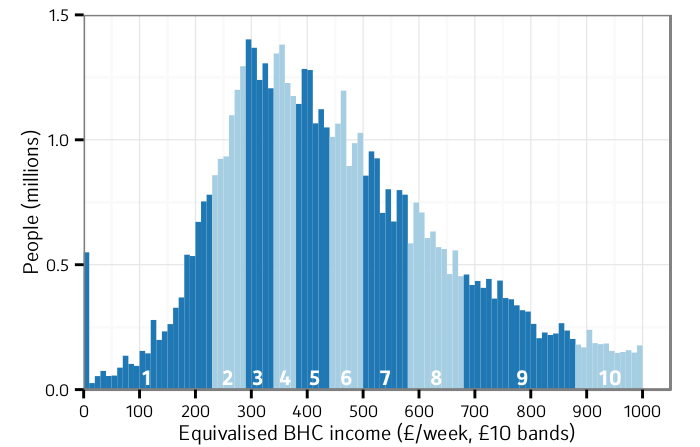
The same approach would be used to create the equivalent chart for AHC income (Chart 2.4/AHC, page 28). Note that the numbers of cases in each band are below what is normally appropriate for use with HBAI, and should not be presented separately. Also note that the numbers in some bands are slightly different to those presented in the main report, because of the rounding of monetary values to the nearest pound in the public-use data from which the chart here is derived.
Poverty rates by social groups (cf Table 3.5db)
Poverty rates can be calculated from HBAI using low-income thresholds
set at various percentages of the population median income, which is
provided in MDOEBHC and MDOEAHC . With this one can look at the
percentage of individuals with various characteristics who are in
low-income households.
### WITHIN-GROUP POVERTY RATES (cf Table 3.5db)
# According to economic status of adults
# A dummy variable for counting whole group populations
hbai$all <- 1
# Whether (at-risk-of) poverty according to various poverty thresholds:
# 50%, 60%, and 70% of median AHC income
hbai$ahc.poor.50 <- ( hbai$S_OE_AHC < hbai$MDOEAHC * 0.5 )
hbai$ahc.poor.60 <- ( hbai$S_OE_AHC < hbai$MDOEAHC * 0.6 )
hbai$ahc.poor.70 <- ( hbai$S_OE_AHC < hbai$MDOEAHC * 0.7 )
# Set up some labels for economic status
econ.statuses <- c("1+ F/T self-employed",
"Single/Couple, all in F/T work",
"Couple, 1 F/T, 1 P/T",
"Couple, 1 F/T, 1 not working",
"No full time, 1+ P/T",
"Workless, 1+ aged 60+",
"Workless, 1+ unemployed",
"Workless, other inactive")
hbai$ad.ec.stat <- factor(econ.statuses[hbai$ECOBU],
levels=econ.statuses)
# Redefine the survey
ppl.svy <- svydesign(id=~1, data=hbai, weight=~GS_NEWPP)
# Calculate the proportion in low income for each threshold & group
eact.pov <- svyby(~ahc.poor.50+ahc.poor.60+ahc.poor.70,
~ad.ec.stat,
design=ppl.svy,
svyratio,
denominator=~all)
# eact.pov
The resulting table can be compared the equivalent one, Table 3.5db of the HBAI publication; in the latest addition this is the Excel spreadsheet additional tables.
| ahc.poor.50/all | ahc.poor.60/all | ahc.poor.70/all | |
| 1+ F/T self-employed | 19 | 25 | 31 |
| Single/Couple, all in F/T work | 4 | 6 | 9 |
| Couple, 1 F/T, 1 P/T | 3 | 7 | 11 |
| Couple, 1 F/T, 1 not working | 14 | 24 | 38 |
| No full time, 1+ P/T | 21 | 31 | 41 |
| Workless, 1+ aged 60+ | 9 | 17 | 28 |
| Workless, 1+ unemployed | 59 | 72 | 80 |
| Workless, other inactive | 36 | 52 | 65 |
Multi-year analysis
HBAI is a continuous series annually from 1994/95, and each package distributed by the UK Data Archive comes with a complete set of files from then to the present date. The dataset as it is distributed is fairly well set-up for analysis of change over time, with one standardised dataset per year. There are some additional considerations when doing analysis over time, notably adjusting for changes in prices.
The income distribution over time (Table 2b, p32)
The values in each annual dataset are in nominal terms, i.e. in the
prices of that year. To compare the real living standard offered by
these amounts between years, the prices need to be adjusted for
inflation to a common
year5. A set of deflators are provided in the User Guide, although
it’s not stated exactly these are derived. A standard consumer price
index (such as ONS CHAX, CPI excluding housing costs) can be used.
### BETWEEN-YEAR COMPARISON OF INCOME DISTRIBUTION
# Set up a dataset to hold information about each year
all.years <- data.frame(
year1=1994:2012,
# The deflators given in the User Guide
ahc.deflator=c(148.8, 153.0, 155.9, 159.0, 159.7,
162.5, 161.8, 164.5, 166.8, 169.4,
171.5, 174.5, 179.8, 184.6, 192.7,
198.8, 209.7, 222.0, 229.5) )
# Give each year its proper label (e.g. "2012/13")
all.years$label <- sapply(all.years$year1,
function(yr)
sprintf("%s/%s",
yr,
substring(sprintf("%i", yr+1), 3, 4 ) ) )
# Find the corresponding data files for each year. There are slight
# variations in how they are named.
all.years$data.file <-
sapply(all.years$year1, function(yr1)
Sys.glob(sprintf("%shbai%s*.tab",
hbai.data.dir,
substring(sprintf("%i",yr1), 3, 4) ) ) )
# Read all the data files in one go and keep them in memory. One could
# also read each file and process in turn.
all.years.data <- sapply(all.years$data.file, read.delim)
# Function to give quintile mid-points and mean of AHC income
yr.quints.and.mean <- function(yr.data) {
svy.ppl <- svydesign(ids=~1,
weights=~GS_NEWPP,
data=yr.data)
c(svyquantile(~S_OE_AHC, svy.ppl, seq(0.1, 0.9, 0.2)),
svymean(~S_OE_AHC, svy.ppl))
}
# Get the nominal (in-year) values and means, for each year
nominal.qiles <- sapply(all.years.data, yr.quints.and.mean)
# Convert all our values to 2012/13 terms (index 229.5)
# = value / source year's index * target year's index
real.qiles <- apply(nominal.qiles, 1,
function(nom.val)
mapply(prod,
nom.val,
1/all.years$ahc.deflator,
229.5) )
# Label and show the output
rownames(real.qiles) <- all.years$label
colnames(real.qiles) <- c(paste("Quintile",1:5), "Mean")
# real.qiles # The result
| Year | Quintile 1 | Quintile 2 | Quintile 3 | Quintile 4 | Quintile 5 | Mean |
|---|---|---|---|---|---|---|
| 1994/95 | 130 | 207 | 304 | 423 | 645 | 367 |
| 1995/96 | 134 | 207 | 304 | 418 | 652 | 369 |
| 1996/97 | 134 | 215 | 319 | 439 | 679 | 385 |
| 1997/98 | 137 | 224 | 326 | 447 | 693 | 397 |
| 1998/99 | 142 | 228 | 333 | 461 | 721 | 413 |
| 1999/00 | 147 | 239 | 346 | 476 | 736 | 426 |
| 2000/01 | 155 | 251 | 360 | 492 | 772 | 449 |
| 2001/02 | 166 | 269 | 381 | 515 | 805 | 470 |
| 2002/03 | 171 | 275 | 391 | 527 | 810 | 477 |
| 2003/04 | 169 | 282 | 394 | 531 | 818 | 479 |
| 2004/05 | 177 | 288 | 399 | 538 | 836 | 491 |
| 2005/06 | 173 | 288 | 403 | 548 | 851 | 498 |
| 2006/07 | 168 | 288 | 408 | 550 | 864 | 504 |
| 2007/08 | 167 | 288 | 410 | 558 | 874 | 513 |
| 2008/09 | 164 | 288 | 405 | 560 | 880 | 512 |
| 2009/10 | 166 | 286 | 406 | 559 | 885 | 516 |
| 2010/11 | 165 | 281 | 392 | 532 | 834 | 484 |
| 2011/12 | 159 | 271 | 377 | 518 | 807 | 472 |
| 2012/13 | 156 | 267 | 374 | 512 | 803 | 462 |
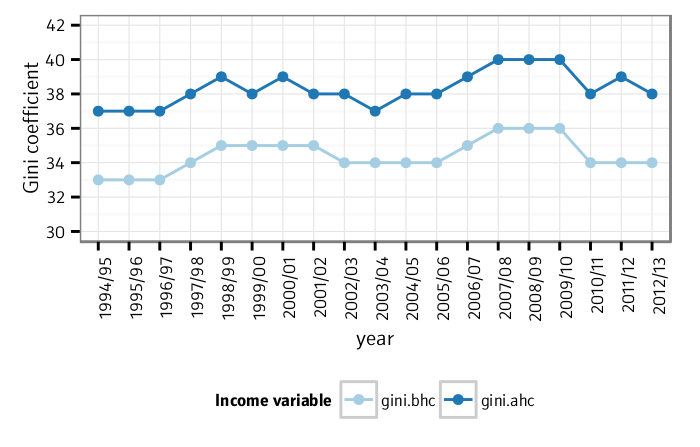
Inequality measures (Chart 2.3, p26)
The published analyses include measures of income inequality over time,
such as the Gini coefficient and the ratio of the 90th decile to the
10th income decile. Here we use R’s reldist package, which is able to
calculate Gini values from weighted data, to reproduce the published
chart of trends in income inequality in Britain 1994 to 2013.
### MEASURES OF INCOME INEQUALITY
# Needed to calculate Gini coefficient from weighted data
library(reldist)
# Calculate BHC and AHC gini (all-people-weighted)
gini.bhc <- sapply(all.years.data,
function(d) gini(d$S_OE_BHC, d$GS_NEWPP))
gini.ahc <- sapply(all.years.data,
function(d) gini(d$S_OE_AHC, d$GS_NEWPP))
# A data frame for plotting
ginis <- data.frame(year=all.years$label,
gini.bhc=gini.bhc,
gini.ahc=gini.ahc)
# In order to convert to "long" format
library(reshape2)
# Note that ggplot2 (rightly) does not allow the use of multiple y-axes,
# so we can't plot the 90/10 ratio on the same chart
ggplot(melt(ginis),aes(x=year, y=round(value*100),
colour=variable, group=variable)) +
geom_path() +
geom_point() +
scale_y_continuous("Gini coefficient",
limits=c(30,42), breaks=seq(30,42,2)) +
scale_colour_brewer("Income variable",
type="qual", palette="Paired") +
theme(axis.text.x = element_text(angle = 90, hjust = 1))
Survey Design & Confidence Intervals
HBAI is a sample survey, and as such estimates from it of quantiles, ratios and so on within the whole population are subject to error (uncertainty). This can be important when, for example, deciding whether changes over time differences between groups are significant. With a total current sample of 20,000, analyses of the whole population in a single year typically have fairly narrow confidence bands. However, for example, the official poverty rate estimates in the HBAI report for regions and ethnic groups are presented using three-year averages (see Charts 3.3 and 3.4, p38).
So far we have treated HBAI as if it were a simple random sample. It actually has a complex multi-stage sampling procedure, which affects sampling error. A recent report discusses the complexities of error calculation in HBAI6. The information about sampling units is not available in the standard public dataset, and bootstrapped calculation of errors is beyond the scope of this note, so the simple method is presented here7.
Confidence intervals of child poverty rates 2012/13 (Table 8b, p104)
The simple method involves calculating confidence intervals as if HBAI were a simple random sample, and then multiplying these by an assumed design factor. A suggested value in the report is 1.3, which is used here.
### ESTIMATING ERROR OF ESTIMATES
# Survey set up, for estimates of children in poverty. As above, this is
# as-if HBAI were a simple random survey. If the PSU and strata
# were known, these would be given with id= and strata=
kid.svy <- svydesign(id=~1,
data=hbai,
weight=~GS_NEWCH)
# Number of children in poverty (ahc.poor.60==TRUE)
kid.tbl <- svytotal(~ahc.poor.60, kid.svy)
# 95% confidence intervals around this total (cf Table 8c)
# confint(kid.tbl)[2,]
# Ratio of children in poverty, with 95% confidence intervals (the
# default). The warning is expected
kid.pov <- svyciprop(~ahc.poor.60,
design=kid.svy,
level=0.95)
# The confidence interval
# confint(kid.pov)
# Returns confidence intervals widened by an arbitrary amount
widened.confint <- function(est, design.factor) {
central.est <- as.numeric(est)
lower.ci <- central.est -
((central.est - confint(est)[1]) * design.factor)
upper.ci <- central.est +
((confint(est)[2] - central.est) * design.factor)
c(lower.ci, upper.ci)
}
# Compare base and assuming a design factor of 1.3
ci.tbl <-rbind(c(cent.est, confint(kid.pov)),
c(cent.est, widened.confint(kid.pov, 1.3)))
# Convert to percentages, add in the published HBAI estimates
ci.tbl <- rbind(ci.tbl * 100,
c(27.4, 26.1, 28.7) )
rownames(ci.tbl) <- c("Assuming SRS design",
"Adjusted by 1.3",
"As published, Table 8b")
colnames(ci.tbl) <- c("Estimate",
"Lower 95% CI",
"Upper 95% CI")
This gives the following main estimates and upper and lower confidence intervals for the estimates. Note that the final confidence intervals calculated here are wider than those published in Table 8b, page 104 of the report, suggesting that in this case the real design factor is less than 1.3.
| Estimate | Lower 95% CI | Upper 95% CI | |
| Assuming SRS design | 27.3 | 25.9 | 28.6 |
| Adjusted by 1.3 | 27.3 | 25.5 | 29.0 |
| As published, Table 8b | 27.4 | 26.1 | 28.7 |
Further reading
The documentation that comes with the dataset, and the fairly lengthy technical appendices to the published reports contain much important information about the design of the survey, such as definitions, classifications, calculations of derived variables and changes to the survey over time. For examples of uses, the Insitute of Fiscal Studies is a well-known major user of the dataset, and their work on the distributional effects of tax and benefit changes are an excellent example of the use of HBAI.
-
I am grateful to Anthony Damico, whose project Analyze Survey Data for Free (http://www.asdfree.com) inspired this note, and whose comments improved it. Any errors are solely my responsibility. ↩
-
Department for Work and Pensions. Households Below Average Income: An analysis of the income distribution 1994/95 – 2012/13 (Published Report & Supporting Tables). 2014. London: Department for Work and Pensions, July 2014. Annex 4, p116f ↩
-
This recent report provides a comprehensive overview: OECD. OECD Framework for Statistics on the Distribution of Household Income, Consumption and Wealth. OECD Publishing, 2013. ↩
-
Department for Work and Pensions. Households Below Average Income, 1994/95-2012/13. 5th ed. 5828 (Dataset). Colchester, Essex: UK Data Archive, 2014. ↩
-
Department for Work and Pensions. Households Below Average Income: An analysis of the income distribution 1994/95 – 2012/13 (Published Report). ↩
-
Department for Work and Pensions. Uncertainty in Family Resources Survey-based analysis. 2014, p. 24. ↩
-
R’s
surveypackage can calculate sampling error for complex survey designs. The documentation is slightly forbidding for non-specialists, but many good examples of the package’s use in R with complex survey designs (mostly from the US) can be found at http://www.asdfree.com. ↩